印度是世界上文化發達最早的地區之一，印度數學的快速神奇也是十分的聞名；那麼印度人在算數學的時候，都會使用印度數學嗎？一個日本青年實在無法壓抑自己的好奇心，竟然真的跑去印度當地，請路人、攤販、店老闆與學生試解一些數學題目，看看這個正在高度成長的國家是不是人人都是使用這種「神器」在算數學。
以14 X12這個題目來說，印度式的計算訓練會先把先把14跟12的個位數2加起來14 + 2 = 16。
再把二個的個位數相乘4 X 2 = 8。
最後把第一步的答案乘以10再加上第二步的答案就行了16 X 10 + 8 = 168
是不是很神奇呢？日本青年也是這樣覺得，下機之後第一位測試者出現了。
遠遠看見了一對印度夫婦，很有禮貌的請他們演示一下14X12這道數學是的解題過程。
這位友善的大叔願意幫忙算。不過…
他拿出NOKIA手機來算…
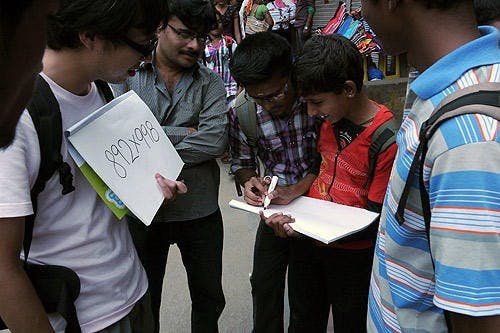
請小學生算…
依算式看來…也是九九乘乘法吧…？！
他們後來去了相當於台灣竹科地位的班加羅爾，想看看在以IT產業聞名的城市裡是否能找到耳聞以久的印度數學。
觀光聖地裡找到二個小哥，不過並不是使用印度數學
大街上賣香蕉的大嬸願意試試
但是她用的是老闆娘的電子計算機…冏RZ
沒關係，路人只能代表市井小民，後來他們又去了班加羅爾的大學裡問問。
來了一個穿著粉紅色的同鞋
啥？又是手機計算機…難不成「印度式數學」意謂著「用計算機來算」的意思嗎？
到大學圖書館裡找一找。
跟管理員表示想要研究「印度式數學」就可以進來了。管理員大叔人真好。
有找到相關的書，但是還是沒有找到人
管理員幫我們找到幾個學生，不過那些學生好像都不是相關科系，所以也沒有學這門課程。
後來連教授都都挖出來了，經過詢問是有印度式數學的存在，不過可能是沒有專任教師在場，所以這趟調查旅行最後還是以「交朋友」做為結束。
若要看日本完整版的文章可以至原始來源網站觀看。
↓↓↓↓↓↓加入癮科技粉絲團，有更多歡樂有趣的科技新聞↓↓↓↓↓↓
